Monotone class theorem
A monotone class in  is a collection
is a collection 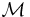 of subsets of
of subsets of  which is closed under countable monotone unions and intersections, i.e. if
which is closed under countable monotone unions and intersections, i.e. if 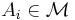 and
and 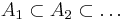 then
then 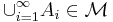 , and similarly for intersections of decreasing sequences of sets.
, and similarly for intersections of decreasing sequences of sets.
The Monotone Class Theorem says that the smallest monotone class containing an algebra of sets 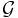 is precisely the smallest σ-algebra containing
is precisely the smallest σ-algebra containing 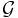 .
.
As a corollary, if 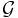 is a ring of sets, then the smallest monotone class containing it coincides with the sigma-ring of
is a ring of sets, then the smallest monotone class containing it coincides with the sigma-ring of 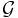 .
.
This theorem is used as a type of transfinite induction, and is used to prove many Theorems, such as Fubini's theorem in basic measure theory.
A functional version of this theorem can be found at PlanetMath.[1]
References: